| VITESSE DE REACTION | ||||||||||||||||||||||||||||||
| Les concentrations [ ] sont exprimées en mole/l Soit la réaction : 2A + 3B ---------> C + 2D La vitesse de cette réaction exprime la variation de concentration des produits ou des réactifs par unité de temps : V(mole/s) = d[C]/dt = d[D]/(2.dt) = -d[A]/(2.dt) = -d[B]/(3.dt)
|
||||||||||||||||||||||||||||||
| Etats de la matière | ||||||||||||||||||||||||||||||
Les réactions en solution permettent d’avoir un mélange intime entre les différents réactifs. Réactions chimiques élémentaires A + B ---------> C + D Pour que 2 molécules A et B réagissent (réaction d’ordre 2), elles doivent se rencontrer avec une certaine vitesse et sous un bon angle (choc efficace), sinon elles rebondissent. Dans le cas d’une réaction élémentaire la vitesse de la réaction dépend de la vitesse de déplacement des particules (donc de la température) et de leurs concentrations : v = kt .[A].[B] Autres réactions élémentaires 2A ---------> C + D qui résulte de la collision de 2 particules A (ordre 2) v = kt .[A]2 A ---------> C + D qui résulte de la décomposition de A (ordre 1) v = kt .[A] |
||||||||||||||||||||||||||||||
| Réactions chimiques complexes |
||||||||||||||||||||||||||||||
| Dans ce cas l’équation chimique ne rend pas compte de la réalité des collisions. Elle n’est en fait qu’un bilan Les réactions d’ordre 1 ou 2 ne sont pas obligatoirement élémentaires. Les réactions d’un ordre supérieur ne le sont jamais (probabilité de collision infime). Une réaction complexe est le bilan de réaction élémentaires. exemple : 2A + B ---------> C + D (réaction complexe) peut être le bilan de : A + B ---------> C + E (réaction élémentaire) La vitesse d’une réaction complexe est déterminée par la vitesse de
l’étape la plus lente. Ainsi si l’étape 1 est la plus lente, Détermination expérimentale de
l’ordre d’une réaction
On trace alors la droite log v = f(log[A]). Sa pente donne n
|
||||||||||||||||||||||||||||||
| Réactions élémentaires réversibles | ||||||||||||||||||||||||||||||
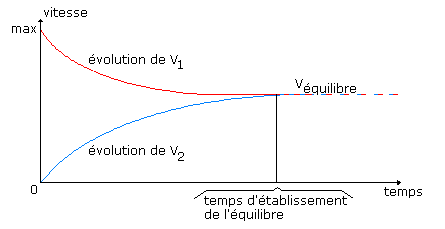
| On introduit A et B dans un réacteur : La réaction peut se faire dans les 2 sens : A + B <---------> C + D V1 est la vitesse dans le sens direct , V2 est la vitesse dans le sens inverse.
A l’équilibre : V1 = V2 par conséquent : k1t.[A].[B] = k2t.[C].[D]
|
||||||||||||||||||||||||||||||
| Réactions complexes réversibles | ||||||||||||||||||||||||||||||
| Soit la réaction réversible en équilibre: 2A + 3B <---------> C + 2D Supposons qu’elle soit le bilan de plusieurs réactions élémentaires. Ces réactions sont obligatoirement des équilibres : Par exemple : A + B
<---------> C
+ E alors k1t.[A].[B] = k2t.[C].[E] On en tire aisément : k1t.k3t.k5t.k7t.k9t.[A]2.[B]3 = k2t.k4t.k6t.k8t.k10t.[C].[D]2
|
||||||||||||||||||||||||||||||
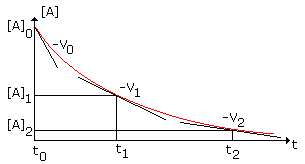 Les réactifs autres que
A sont mis en excès de manière à ce que leur concentration puisse être considérée
comme constante au cours de l’évolution de la réaction. L’équation de vitesse
devient alors v = K. [A]n. On trace la courbe [A] = f(t) et on détermine
graphiquement la valeur de v en quelques points :
Les réactifs autres que
A sont mis en excès de manière à ce que leur concentration puisse être considérée
comme constante au cours de l’évolution de la réaction. L’équation de vitesse
devient alors v = K. [A]n. On trace la courbe [A] = f(t) et on détermine
graphiquement la valeur de v en quelques points :